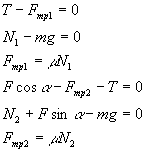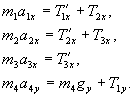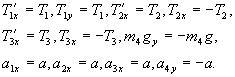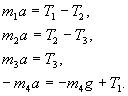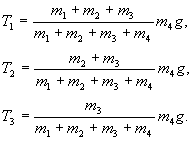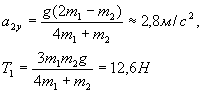На этом уроке нам предстоит научиться решать физические задачи, в основе которых лежат законы Ньютона. Иначе эти задачи называются динамическими задачами. Основные принципы решения таких задач те же, что изложены во втором уроке, но конкретная реализация этих принципов имеет свои особенности.

Итак, первый этап – постановка задачи. Он включает в себя пять пунктов:

Действительно, пусть на нить действуют силы и . Согласно второму закону Ньютона . Так как масса нити считается равной нулю, то  и .

По третьему закону Ньютона одинаковы и силы, с которыми нить действует на прикрепленные к ней тела.

Массой всех блоков, встречающихся в условиях, также будем пренебрегать. В этом случае натяжение перекинутой через блок 

нити можно считать одинаковым по обе стороны блока. В противном случае натяжение нити по обе стороны блока будет различным. За счет различия в натяжении угловая скорость блока, обладающего массой, будет изменяться.

На этом заканчивается постановка динамической части задачи. Если в задаче требуется найти не только силы или ускорения, но также скорости и координаты, то требуется дополнить задачу кинематической частью. Как решать задачи по кинематике, описано во Втором Открытом уроке.

На этом заканчивается этап постановки задачи. Мы выполнили работу физика. Теперь необходимо перейти в состояние математика и решить полученную нами систему уравнений. Это второй этап, математический. Получив решение задачи в общем виде, необходимо перейти в состояние физик и заняться анализом решения. Прежде всего, необходимо проверить размерность. Такая проверка поможет обнаружить возможную ошибку в расчетах.

Полезно проследить, как будут меняться найденные величины при варьировании величин, заданных в условии задачи. Если, к примеру, окажется, что при некоторых значениях заданных в условиях величин искомая величина обращается в бесконечность, то это указывает обычно на ошибку в решении или на неприменимость использованной физической модели. Это третий этап, анализ решения. Видно, что наиболее сложным и ответственным является первый этап, этап постановки задачи. На этом этапе в основном и требуются ваши способности физика.

В начале, когда вы только обучаетесь решению задач, необходимо осознанно выполнять каждый пункт этого алгоритма. В дальнейшем, когда вы станете мастерами в решении задач, отдельные пункты можно будет не писать на бумаге, держа их в подсознании. Вспомним слова Р. Фейнмана: “Физик – это тот, кто видит решение задачи, не решая ее”. К этому можно прийти, прорешав несколько тысяч задач. Это немного, 3 – 4 задачника.

Рассмотрим задачу, которая проиллюстрирует нам пятый пункт стадии “Постановка задачи”.

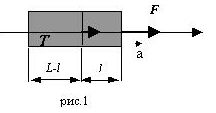
Задача 1. Однородный стержень длиной L и массой m движется по гладкой горизонтальной плоскости под действием силы , приложенной к торцу стержня и направленной вдоль оси стержня (рис. 1). Определите натяжение стержня в сечении, отстоящем от этого торца на l.

Сила является единственной горизонтальной силой, действующей на стержень. Под действием этой силы стержень движется с ускорением , которое легко найти, используя второй закон Ньютона. Направим координатную ось Х вдоль оси стержня в сторону действия силы. В проекциях на эту ось второй закон Ньютона имеет вид

Мысленно отсечем от стержня переднюю часть длиной l. Оставшаяся часть имеет длину  и массу . Эта часть стержня движется с тем же ускорением , что и весь стержень, под действием искомой силы натяжения . Запишем для нее второй закон Ньютона в проекциях на ось Х:

На этом стадия постановки задачи заканчивается. Соединим, в знак этого, уравнения (1) и (2), фигурной скобкой. Переходим из состояния физик в состояние математик и приступаем к решению полученной системы уравнений. В результате получаем

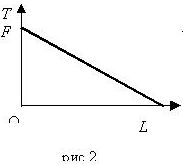
Приступаем к третьему этапу – анализ решения. Переходим в состояние физик.

Видно, что размерность в уравнении (3) слева и справа имеет размерность силы, т.е. в системе СИ – ньютон. Это хороший довод в пользу того, что мы не ошиблись при решении.

Далее, из уравнения (3) видно, что натяжение линейно убывает от максимального значения F до нуля с увеличением расстояния lот нуля до L (рис. 2).

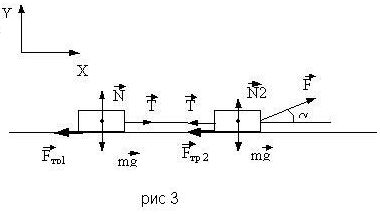
Таким образом, если речь в задаче будет идти о нити или тросе, масса которых не является пренебрежимо малой, то необходимо учитывать изменение натяжения при переходе от одного сечения к другому.

Задача 2. Человек везет двое связанных саней, прикладывая силу под углом 30⁰ к горизонту. Найдите эту силу, если известно, что сани движутся равномерно. Массы саней по 40 кг. Коэффициент трения 0,3.

Читаем условие задачи. В задаче не указано, движутся ли сани равномерно или ускоренно. Так как эту задачу не решить без знания величины ускорения, примем, что ускорение равно нулю, т.е. сани движутся равномерно. Далее, не указано, направлена ли веревка вверх или вниз. При заданном в задаче значении коэффициента трения m это несущественно, если бы угол или m были больше, то возможно явление заклинивания, если сила направлена вниз, и этого явления нет, если сила направлена вверх. Примем, что сила направлена вверх. Если подобная ситуация возникнет на экзамене или олимпиаде и вы увидите, что условие задачи толкуется неоднозначно, то следует обсудить и решить все возможные варианты.

Делаем рисунок. Так как мы принимаем, что веревка, связывающая сани, невесома и нерастяжима, то мы сразу рисуем одинаковые силы натяжения Т, приложенные к саням от натянутой веревки.

Так как сани движутся с постоянной скоростью, то по первому закону Ньютона сумма сил, действующих на сани, равна нулю. Запишем первый закон Ньютона для каждого тела сразу в проекции на оси:

Мы добавили к уравнениям первого закона Ньютона уравнения Кулона для сухого трения, так как известно, что сани скользят.

На этом мы закончили этап постановки задачи, переходим из состояния физик в состояние математик и решаем полученную систему уравнений.

Получаем

Если бы мы направим силу F вниз, то в знаменателе перед появится минус, и при  знаменатель обращается в нуль. Это означает, что тело не может сдвинуться при любой величине силы F.

Эта задача решалась в задачнике Черноуцана, задача №10, глава 2, “Динамика”. Задачка решалась неверно, предполагалось, что сила F приложена сразу к двум связанным в одно тело санкам. Но ответ получился такой же, как и у нас. Подумайте, почему это произошло. Может быть, стоит доказать теорему: если тело разделить на n тел, связанных между собой нитями, то сила трения, возникающая при движении этого тела равна сумме сил трения, действующих на связку n движущихся тел?

Задача 3. На гладкой горизонтальной поверхности расположены три тела массами m_1, m₂ и m₃, связанные нерастяжимыми нитями друг с другом (рис 4а). К телу массой m₁ прикреплена перекинутая через блок нить, на конце которой находится груз массой m₄.. Найдите модули ускорений тел системы и натяжений всех нитей. Массами нитей и блока пренебречь.

Изобразим все силы, действующие на тела (рис 4б). Силы, действующие по вертикали на тела массами m_1, m₂ и m₃ взаимно уравновешиваются, и их рассмотрение не требуется для решения задачи. Если бы в задаче действовали силы трения, то нам потребовалось бы написать уравнения проекций этих сил на осьY, чтобы получить N₁, N₂, N₃, нужные нам для определения сил трения.

Ось Х направим горизонтально слева направо, а ось Y – вертикально вверх.

Уравнения движения для проекций ускорений и сил (второй закон Ньютона) на оси Х и Y для всех четырех тел будут иметь вид:

Нити нерастяжимы, поэтому . Так как массами нитей и блока пренебрегаем, то с учетом направления осей Х и Y имеем

Тогда уравнения движения запишутся следующим образом:

На этом заканчивается этап постановки задачи, мы становимся математиками и решаем полученную систему уравнений. Такую систему можно решать методом подстановки, но изящнее было бы сложить первые три уравнения и отнять четвертое. Тогда сразу получим

Подставляя найденное значение ускорения поочередно во все уравнения движения, начиная с последнего, получим

На этом заканчивается математический этап, и мы приступаем к анализу решения. Первым делом проверяем размерности. Видно, что размерность a совпадает с размерностью g. Размерности Т имеют размерность mg, т.е. размерность силы. Порядок.

Обратим внимание, что натяжение Т₁ первой нити не равно , как это было бы для покоящегося тела, а меньше в отношении

Как и следовало ожидать, , так как нити сообщают одинаковые ускорения разным массам.

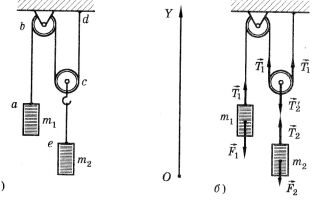
Задача 4. Найдите натяжения Т₁ и Т₂ нитей abcd и ce в устройстве с подвижным блоком, изображенном на рис 5а. Массы тел соответственно равны m₁ = 3 кг и m₂ = 2 кг.

Так как массой нитей и блоков можно пренебречь, то натяжение нитей одинаково во всех сечениях. Нить abcd, огибающая блоки, действует на тело m₁ и на левую и правую стороны подвижного блока с одинаковой силой  (рис 5б). Нить ce, соединяющая тело массой m₂ с подвижным блоком, действует на них с одинаковыми по модулю силами .

Координатную ось Y направим вверх. Учитывая, что получим следующую систему уравнений:

Последнее уравнение написано для подвижного блока с учетом того, что его масса равна нулю.

Система трех уравнений содержит четыре неизвестных: . Необходимо добавить уравнение кинематической связи

Мы получили систему из четырех уравнений для четырех неизвестных. На этом стадия постановки задачи заканчивается. Дальше мы, став на время математиками, решаем эту систему уравнений и получаем:

Учитывая, что  получим Т₂ = 25,2 Н. Так как  то ускорение  направлено вверх.

Проекция ускорения первого тела  Знак минус у проекции ускорения  показывает, что ускорение первого тела направлено противоположно оси , т.е. вниз.

Домашнее задание:

Из базового задачника: с 2.1 до 2.27 нечетные.

Задание для физиков:

Задача 1. На горизонтальной доске длиной l лежит груз массой m. Коэффициент трения между грузом и доской равен m . Через какое время груз соскользнет с доски, если доска движется с ускорением (рис 6).

Ответ:.

Задача 2. Какую силу F должен приложить человек массой m, чтобы сдвинуть с места ящик массой M? Коэффициент трения о пол человека и ящика одинаковы и равны m. Считать M> m.

Ответ:

Задача 3. Мальчик вращает в вертикальной плоскости камень на нити длиной 1,2 м. После обрыва нити камень летит вертикально вверх. На какую максимальную высоту поднимется камень, если в момент отрыва полное ускорение камня было направлено под углом 45⁰ к вертикали?

Ответ: 

Задача 4. На подставке лежит тело, подвешенное к потолку с помощью пружины. В начальный момент пружина не растянута. Подставку начинают опускать вниз с ускорением а. Через какое время Dt тело оторвется от подставки? Жесткость пружины k, масса тела m.