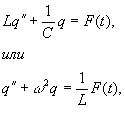Физика для абитуриента. Решение задач по физике для поступающих в ВУЗ.
Вопросы и консультации.
О сайте
Порядок работы
Новости сайта
Контакт
 
Приёмная комиссия. 
Вступительное задание. 
Открытые уроки. 
Учебники по физике. 
Задачи по физике. 
Справочник по физике. 
Вопросы и консультации. 
Рефераты.
Олимпиады и турниры по физике. 
Современная физика. 
Весёлая наука. 
Воскресная школа.
Уголок крохобора. 
Не только физика. 
Директория ссылок. 
Репетиторы. 
Малая академия наук.

.

info@abitura.com

 Ответы на вопросы по физике. Буров Ю.М.

Предыдущие страницы смотрите здесь.

Коробков Игнат Санкт-Петербург.(студент)
Доброе время суток .
У меня вопрос ...
Вывод формул :
1)Собственной частоты контура
2)Частоты затухания
3)Резонансной частоты для q
4)Резонансной частоты для тока

Игнат, извините, но это не те вопросы, которые можно разбирать в Интернете. Есть хорошие учебники, а еще лучше воспользоваться лекциями. Поищите конспект лекций вашего лектора. Это самый надежный путь.

Можно тогда хотябы вывод формулы
резонансной частоты для тока ...
(хотябы в общем...)

Я не знаю, каким методом вам излагали этот материал на лекциях. А на экзамене желательно отвечать именно так, как это делал сам преподаватель. Поэтому настоятельно рекомендую найти конспект лекций. А так, возможны варианты. Например, согласно учебнику “Физика 11” Глазунова,Кабардина и др. с помощью векторных диаграмм выводят закон Ома для цепи переменного тока, а на странице 31 рассматривают

Задачу 2

В колебательный контур последовательно включен источник синусоидального переменного напряжения. При каких частотах достигается максимальное значение амплитуд колебаний силы тока и напряжения на обкладках конденсатора?

Предлагается такое решение:

Из закона Ома для цепи переменного тока

Вопросы и консультации по физике. Решение задач по физике. Лекции, конспект лекций, колебательный контур, сила тока, напряжение, закон Ома, дифференциальные уравнения, решение дифференциальных уравнений, решение однородного уравнения, интеграл, резонанс, правило Лопиталя, колебания

следует, что сила тока достигает максимального значения при выполнении условия:

Вопросы и консультации по физике. Решение задач по физике. Лекции, конспект лекций, колебательный контур, сила тока, напряжение, закон Ома, дифференциальные уравнения, решение дифференциальных уравнений, решение однородного уравнения, интеграл, резонанс, правило Лопиталя, колебания

Напряжение на обкладках конденсатора напряжение на обкладках конденсатора равно:

Вопросы и консультации по физике. Решение задач по физике. Лекции, конспект лекций, колебательный контур, сила тока, напряжение, закон Ома, дифференциальные уравнения, решение дифференциальных уравнений, решение однородного уравнения, интеграл, резонанс, правило Лопиталя, колебания

Исследуя полученное выражение на максимум, получаем:

колебания, резонанс, колебательный контур,

где добротность колебательного контура, колебания - добротность контура.

Так эта задачка решается в школе. Но так как вы уже студент ВУЗа, то вам не прилично отвечать на таком уровне. Предположу, что вам уже давали дифференциальные уравнения. Тогда запишем закон сохранения энергии для колебательного контура:

Вопросы и консультации по физике. Решение задач по физике. Лекции, конспект лекций, колебательный контур, сила тока, напряжение, закон Ома, дифференциальные уравнения, решение дифференциальных уравнений, решение однородного уравнения, интеграл, резонанс, правило Лопиталя, колебания

Продифференцируем правые и левые части этого уравнения и получим

Вопросы и консультации по физике. Решение задач по физике. Лекции, конспект лекций, колебательный контур, сила тока, напряжение, закон Ома, дифференциальные уравнения, решение дифференциальных уравнений, решение однородного уравнения, интеграл, резонанс, правило Лопиталя, колебания

где мы ввели частоту колебания, колебательный контурсвободных колебаний и функцию колебания, колебательный контур, резонанс, аналог внешней силы в механических колебаниях.

Как известно, общее решение неоднородного линейного дифференциального уравнения с постоянными коэффициентами получаем в виде суммы двух выражений: Вопросы и консультации по физике. Решение задач по физике. Лекции, конспект лекций, колебательный контур, сила тока, напряжение, закон Ома, дифференциальные уравнения, решение дифференциальных уравнений, решение однородного уравнения, интеграл, резонанс, правило Лопиталя, колебания где решение дифференциального уравнения- общее решение однородного уравнения, а чачтный интеграл неоднородного дифференциального уравнения - частный интеграл неоднородного уравнения. В данном случае Вопросы и консультации по физике. Решение задач по физике. Лекции, конспект лекций, колебательный контур, сила тока, напряжение, закон Ома, дифференциальные уравнения, решение дифференциальных уравнений, решение однородного уравнения, интеграл, резонанс, правило Лопиталя, колебания описывает свободные колебания.

Рассмотрим имеющий особый интерес случай, когда вынуждающая сила является простой периодической функцией времени с некоторой частотой колебания, колебательный контур:

Вопросы и консультации по физике. Решение задач по физике. Лекции, конспект лекций, колебательный контур, сила тока, напряжение, закон Ома, дифференциальные уравнения, решение дифференциальных уравнений, решение однородного уравнения, интеграл, резонанс, правило Лопиталя, колебания.

Частный интеграл ищем в виде интеграл. Подстановка в уравнение дает: дифференциальные уравнения, прибавляя решение однородного уравнения, получим общий интеграл в виде

Вопросы и консультации по физике. Решение задач по физике. Лекции, конспект лекций, колебательный контур, сила тока, напряжение, закон Ома, дифференциальные уравнения, решение дифференциальных уравнений, решение однородного уравнения, интеграл, резонанс, правило Лопиталя, колебания. (*)

Таким образом, под действием периодической вынуждающей силы в колебательном контуре возникают колебания, которые представляют собой совокупность двух колебаний – с собственной частотой системы колебания, колебательный контур, частота и с частотой вынуждающей силы колебательный контур, резонанс.

Полученное решение неприменимо в случае так называемого резонанса, когда частота вынуждающей силы совпадает с собственной частотой системы. Для нахождения общего решения в этом случае перепишем выражение (*) с соответствующим переобозначением постоянных в виде

Вопросы и консультации по физике. Решение задач по физике. Лекции, конспект лекций, колебательный контур, сила тока, напряжение, закон Ома, дифференциальные уравнения, решение дифференциальных уравнений, решение однородного уравнения, интеграл, резонанс, правило Лопиталя, колебания.

При колебательный контур, резонанс второй член дает неопределенность вида правило Лопиталя. Раскрывая ее по правилу Лопиталя, получим:

Вопросы и консультации по физике. Решение задач по физике. Лекции, конспект лекций, колебательный контур, сила тока, напряжение, закон Ома, дифференциальные уравнения, решение дифференциальных уравнений, решение однородного уравнения, интеграл, резонанс, правило Лопиталя, колебания.

Таким образом, в случае резонанса амплитуда колебаний растет линейно со временем (до тех пор, пока колебания не перестанут быть малыми и вся излагаемая теория престанет быть применимой).

И еще раз рекомендую обратиться к друзьям и подругам, найти конспект и излагать материал близко к лекционному. Среди преподавателей очень часто встречаются особы, для которых экзамены – это возможность продемонстрировать свое превосходство. К этому надо относиться с пониманием и не подставляться.
 

 
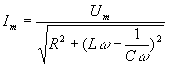
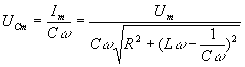
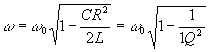Следующие страницы смотрите здесь.
Обсудить на форуме.


Fatal error: Uncaught Error: Call to undefined function set_magic_quotes_runtime() in /www/htdocs/1dbcf2b3552b065fc49d8747114db86c/sape.php:262 Stack trace: #0 /www/htdocs/1dbcf2b3552b065fc49d8747114db86c/sape.php(343): SAPE_base->_read('/www/htdocs/1db...') #1 /www/htdocs/1dbcf2b3552b065fc49d8747114db86c/sape.php(418): SAPE_base->load_data() #2 /www/htdocs/links.html(7): SAPE_client->SAPE_client() #3 /www/htdocs/questions/otv_burov_3o.html(218): include('/www/htdocs/lin...') #4 {main} thrown in /www/htdocs/1dbcf2b3552b065fc49d8747114db86c/sape.php on line 262