Вступительное задание.
Открытые уроки.
Учебники по физике.
Задачи по физике.
Справочник по физике.
Вопросы и консультации.
Рефераты.
Олимпиады и турниры
по физике.
Современная физика.
Весёлая наука.
Воскресная школа.
Уголок крохобора.
Не только физика.
Директория ссылок.
Репетиторы.
Малая академия наук.
.
info@abitura.com
|
Ответы на вопросы по физике. Буров Ю.М.
Предыдущие страницы смотрите здесь.
Капилярные явления.
Задача 1. Керосин вытекает из отверстия трубки диаметром 1,8 мм. Сколько капель получится из 1 кубического сантиметра керосина?
В школьной и даже институтской физике такие задачи решаются следующим образом. Считается, что в момент отрыва капли вес капли равен силе поверхностного натяжения по линии касания капли с трубкой. Вес капли равен 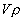 , сила поверхностного натяжения равна , сила поверхностного натяжения равна 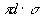 . Отсюда найдем объем капли, а, разделив 1 см3 на объем одной капли, найдем число капель. Сейчас уже не помню, то ли в школе, то ли в МИФИ мне приходилось делать лабораторную работу, где определялся коэффициент поверхностного натяжения по весу капель. Полученная величина хорошо совпала с табличным значением . Отсюда найдем объем капли, а, разделив 1 см3 на объем одной капли, найдем число капель. Сейчас уже не помню, то ли в школе, то ли в МИФИ мне приходилось делать лабораторную работу, где определялся коэффициент поверхностного натяжения по весу капель. Полученная величина хорошо совпала с табличным значением 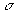 . Но если вы внимательно присмотритесь к процессу отрыва капли от трубки, то увидите, что капля отрывается не по линии контакта, а путем постепенного утончения перешейка. Я попробовал изобразить это на рисунке. То есть отрыв капли происходит по другому механизму, а совпадение результатов, скорее всего случайное. Механизм отрыва капли следующий. . Но если вы внимательно присмотритесь к процессу отрыва капли от трубки, то увидите, что капля отрывается не по линии контакта, а путем постепенного утончения перешейка. Я попробовал изобразить это на рисунке. То есть отрыв капли происходит по другому механизму, а совпадение результатов, скорее всего случайное. Механизм отрыва капли следующий.
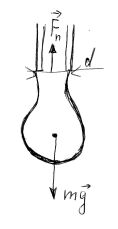
Столбик жидкости создает внизу давление, равное 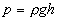 . Пленка поверхностного натяжения создает давление, равное . Пленка поверхностного натяжения создает давление, равное 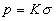 . .
К – кривизна поверхности. О кривизне поверхности можно прочитать в книге Д.Гильберта, С. Кон-Фоссена “Наглядная геометрия”. Замечательная книга! При некотором размере капли возникает перешеек. В процессе отрыва капли кривизна поверхности в области перешейка уменьшается, радиус перешейка постепенно уменьшается до нуля, капля отрывается от трубки, а, точнее, от жидкости, прилипшей к концу трубки.
Задача 2. В капиллярной трубке жидкость поднимается на 80 см. Определить высоту столбика жидкости, которая может удержаться в трубке, если ее полностью заполнить жидкость в горизонтальном положении, а затем повернуть вертикально.
Составитель задачи, видимо полагал, что ответ должен быть 160 см. Действительно, вес столба жидкости равен силе капиллярного притяжения между мениском и трубкой, направленной вверх. Когда трубка вынута из жидкости, на жидкость действуют уже две силы, одна на верхнем мениске, другая - на нижнем. Если бы внутренний радиус трубки вверху был бы равен внешнему радиусу трубки внизу, то капиллярные силы увеличиваются вдвое, и потому вдвое должна увеличиться высота столба жидкости. Как видите, нам пришлось ввести неочевидное предположение о равенстве радиусов трубки, которого нет в условие задачи. Похожая задача рассмотрена в учебнике физики Г.Я. Мякишева и А.З. Синякова. Задача решается с использованием формулы, описывающей давление капиллярной пленки через ее кривизну, но, к сожалению, не дано правильное определение кривизны поверхности. Найдите и прочитайте “Наглядную геометрию” Д.Гильберта, С. Кон-Фоссена. Очень хорошая книга!
Следующие страницы смотрите здесь.
Fatal error: Uncaught Error: Call to undefined function set_magic_quotes_runtime() in /www/htdocs/1dbcf2b3552b065fc49d8747114db86c/sape.php:262
Stack trace:
#0 /www/htdocs/1dbcf2b3552b065fc49d8747114db86c/sape.php(343): SAPE_base->_read('/www/htdocs/1db...')
#1 /www/htdocs/1dbcf2b3552b065fc49d8747114db86c/sape.php(418): SAPE_base->load_data()
#2 /www/htdocs/links.html(7): SAPE_client->SAPE_client()
#3 /www/htdocs/questions/otv_burov_3g.html(162): include('/www/htdocs/lin...')
#4 {main}
thrown in /www/htdocs/1dbcf2b3552b065fc49d8747114db86c/sape.php on line 262
|

