На этом уроке мы будем рассматривать круговые процессы, совершаемые с рабочим телом, в нашем случае – с идеальным газом. При этом рабочее тело на разных этапах участвует в различных квазистационарных процессах, переходя из одного равновесного состояния в другое, и в конечном итоге возвращается в исходное состояние. На диаграммах такие процессы изображаются замкнутыми линиями.

   Устройство, в котором круговой процесс, изображенный на pV- диаграмме, идет по часовой стрелке, называют тепловой машиной. Поскольку изменение внутренней энергии при круговом процессе равно нулю (внутренняя энергия является функцией состояния), алгебраическая сумма количеств теплоты, подводимых к рабочему телу, равна работе, совершаемой рабочим телом за цикл (первый закон термодинамики).

   Если суммарное подводимое к рабочему телу количество теплоты обозначить через Q₁, а суммарное количество отводимого тепла через Q₂, то работа, совершенная рабочим телом, равна

   Эффективность работы тепловой машины принято характеризовать коэффициентом полезного действия (КПД):

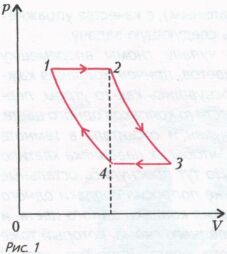
   Поскольку в случае тепловой машины Q₁ >Q₂, то h< 1.

   Если круговой процесс происходит в обратном направлении, против часовой стрелки на pV- диаграмме, т.е. устройство работает как холодильная машина или тепловой насос, тепловые потоки изменяют свои направления: там, где раньше рабочее тело отдавало тепло, теперь получает его от внешнего резервуара, а там, где получало, теперь отдает тепло. Таким образом, уже не рабочее тело совершает работу, равную разности подводимых и отводимых количеств теплоты, а за счет внешней работы, совершаемой над рабочим телом, тепло, отбираемое от внешнего тела с меньшей температурой (холодильника), передается внешнему телу с большей температурой (нагревателю). Тепловой насос оказывается более эффективным устройством для обогрева помещений, чем электрические нагреватели с коэффициентом полезного действия в 100%. Количество тепла Q₂, полученное с помощью теплового насоса, равно

   Получается, что КПД теплового насоса, работающего в качестве нагревателя, больше 100%. В свое время это обстоятельство очень удивило инженеров и обсуждалось в журнале “Техника – молодежи”. Несмотря на высокую тепловую эффективность тепловых насосов широкого применения в качестве обогревателей помещений они пока не получили. Еще не удалось найти хорошую конструкцию, достаточно простую, надежную и дешевую. Но изобретатели и инженеры продолжают свои поиски, и, возможно, в недалеком будущем, батареи центрального отопления в наших домах заменят тепловые насосы, перекачивающие тепло из морозного воздуха улицы внутрь теплой комнаты. 

   Перейдем к решению конкретных задач. Лучший способ изучения физики – решение задач по физики.

   Задача 1. На диаграмме зависимости давления p от объема V для некоторой массы идеального газа две изотермы пересекаются двумя изобарами в точках 1, 2, 3 и 4 (рис. 1). Найдите отношение температурТ₃/Т₁ в точках 3 и 1, если отношение объемов в этих точках V₃/V₁= a. Объемы газа в точках 2 и 4 равны.

   Рассмотрим изобарические участки.
Уравнение изобары имеет вид V/T = const.
Для состояний 1 и 2, и для состояний 3,4 имеем

где Т₁ и Т_{2 –} температуры газа на изотермах 4 – 1 и 2 – 3,а V₁и V₂ – объемы газа в состояниях 1 и 2. Аналогичное соотношение для состояний 3 и 4 будет иметь вид

где V₃и V₄ – объемы газа в состояниях 3 и 4. Добавим два очевидных соотношения и получим следующую систему уравнений:

   Решать систему уравнений можно различными способами, но удобно из третьего и четвертого уравнений выразить отношение Т₃/Т₁ и равное ему Т₂/Т₁, перемножить почленно и получить

откуда

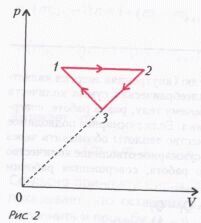
   Задача 2. На рисунке 2 для n молей гелия показан цикл, состоящий из двух участков линейной зависимости давления p от объема V и изобары. На изобаре 1–2 газ совершил работу А, и его температура увеличилась в 4 раза. Температуры в состояниях 1 и 3 равны. Точки 2 и 3 на pV-диаграмме лежат на прямой, проходящей через начало координат. Определите температуру газа в точке 1. Определите также работу газа за цикл.

   Обозначим температуру гелия в состоянии 1 через Т₁, тогда температура в состоянии 2 будет равна 4Т₁. 

Пусть давление на изобаре 1-2 равно p₁, тогда работа, которую совершил газ при изобарическом процессе, равна

где V₁ и V₂ – объемы гелия в состояниях 1 и 2. Поскольку

то 

Отсюда

Работу газа за цикл вычислим по площади треугольника 123:

,
где p₃– давление газа в состоянии 3.
Из уравнения состояния для идеального газа найдем

, 

.

После подстановки значений V₁ и V₂ в выражение для работы газа за цикл получим

.

Так как на нашей pV-диаграмме точки 2 и 3 лежат на прямой, проходящей через начало координат, можно записать соотношение

.

Поскольку

и ,

то

.

Отсюда

,

и окончательно

.

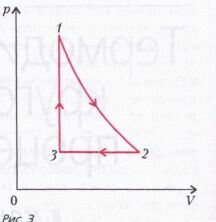
Задача 3. Найдите работу А, которую совершает моль гелия в замкнутом цикле, состоящим из адиабаты 1-2, изобары 2-3 и изохоры 3-1(рис. 3). В адиабатическом процессе разность максимальной и минимальной температур газа равна D Т. В изобарическом процессе от газа отвели количество теплоты Q.

Рассмотрим адиабатический процесс 1-2. Процесс идет с увеличением объема газа, следовательно, газ совершает работу. В адиабатическом процессе работа, совершаемая газом, численно равна изменению внутренней энергии газа, взятому с противоположным знаком, следовательно, температура газа уменьшается. В состоянии 1 температура максимальна, а в состоянии 2 – минимальна, поэтому можно записать

Рассмотрим изобарический процесс 2-3. По первому началу термодинамики можно записать

где  - молярная теплоемкость гелия при постоянном объеме, р_{2 –} давление газа в изобарическом процессе 2-3. Отсюда с учетом соотношений  и , получим

На изохорическом участке 3-1 работа газом не совершается, а увеличение внутренней энергии газа происходит за счет подвода тепла:

Работа, совершаемая молем газа в заданном цикле, равна

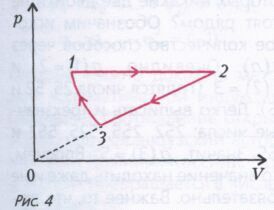
Задача 4. Газообразный гелий находится в цилиндре под подвижным поршнем. Газ нагревают при постоянном давлении, переводя его из состояния 1 в состояние 2 (рис. 4). При этом газ совершает работу А₁₂. Затем газ сжимают в процессе 2-3, когда его давление р прямо пропорционально объему V. При этом над газом совершается работа А₂₃ (А_{23 >}0).Наконец, газ сжимается в адиабатическом процессе 3-1, возвращаясь в первоначальное состояние. Найдите работу сжатия А₃₁, совершаемую над газом в адиабатическом процессе.

Введем обозначения: температуры и объемы в состояниях 1,2 и 3 обозначим через Т_1, Т₂ ,Т₃ и V₁, V₂ и V₃, давление на изобаре 1-2 через p₁, в состояниях 2 и 3 как p₂ и p₃, работы на участках 1-2, 2-3 и 3-1 через А₁₂, А₂₃ и А₃₁, n- число молей гелия.

Запишем выражения для работы на участках 1-2, 2-3 и 3-1.

На pV-диаграмме точки 2 и 3 лежат на прямой, проходящей через начало координат, следовательно,

и выражение для работы A₂₃ приобретает вид

Полученную систему можно решать различными способами, но удобно выразить T₂ –T₁ из первого уравнения, T₂ –T₃ из последнего, получить T₁ –T₃ и подставить в А_31. Окончательно имеем
 
 

Задача 5. КПД тепловой машины, работающей по циклу, состоящему из изотермы 1-2, изохоры 2-3 и адиабатического процесса 3-1 (рис. 5), равен h , а разность максимальной и минимальной температур газа в цикле равна DТ. Найдите работу, совершенную n молями идеального одноатомного газа в изотермическом процессе.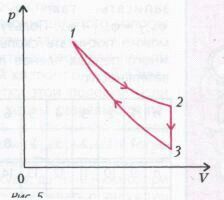

Нам задан КПД цикла, поэтому сначала разберемся, на каких участках цикла тепло подводится к газу, а на каких отводится.

На изотермическом участке 1-2 газ совершает работу (происходит увеличение объема), а поскольку внутренняя энергия газа не изменяется (почему?), то работа газа совершается за счет подвода тепла. Обозначим подведенное количество тепла через Q₁.

На изохоре 2-3 при постоянном объеме происходит падение давления. Очевидно, что это осуществляется за счет уменьшения температуры газа, и в этом случае тепло отводится от газа. Обозначим отведенное количество тепла через Q₂.

На адиабатическом участке 3-1 не отводится и не подводится, а с уменьшением объема над газом совершается работа, и его температура растет. 

Следовательно, в точке 3 газ имеет наименьшую температуру T_min, а максимальная температура T_max газа была на изотерме 1-2. Таким образом,

Поскольку речь идет о КПД, запишем определение КПД замкнутого цикла:

На изотермическом участке

.

Решив эту систему уравнений, получим

Задача 6. КПД цикла 1-2-4-1 равен h₁, а цикла 2-3-4-2 равен h₂ (рис. 6). Найдите КПД цикла 1-2-3-4-1. Участки 4-1 и 2-3 изохоры, участок 3-4 изобара, участки 1-2 и 2-4 представляют линейную зависимость давления от объема. Все циклы обходятся по часовой стрелке. Рабочее вещество – идеальный газ.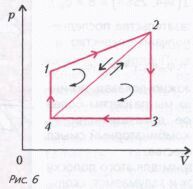

Рассмотрим цикл 1-2-4-1. На участке 1-2 тепло подводится к газу (почему?). Обозначим подведенное количество теплоты через Q₁. На участке 2-4 тепло отводится (почему?). Обозначим его через Q₂. Подводимое (почему?) к газу на изохорическом участке 4-1 количество теплоты обозначим через Q₃. Если обозначить работу, совершаемую газом в этом цикле через А₁, то КПД цикла равен

С другой стороны,

откуда получим

Теперь рассмотрим цикл 2-3-4-2. На участках 2-3 и 3-4 тепло отводится от газа (почему?). Подводится тепло только на участке 4-2 и подведенное количество теплоты, очевидно, равно Q₂. КПД данного цикла равен

где А₂ – работа, совершаемая газом в этом цикле. Используя выражение для Q₂, можно записать

КПД цикла 1-2-3-4-1 равен

Выразив А₁ и А₂ из выражений для h₁ и h₂, получим

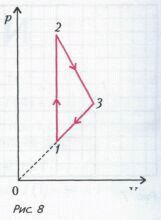
Домашнее задание:

Из Базового задачника задачи 8.94 –8.98.

Из Задачника для физиков:

Задача 1. На pV- диаграмме для некоторой массы идеального газа две изобары и две изохоры пересекаются в точках 1,2,3 и 4 (рис. 7). Найдите температуры газа Т₁ и Т₃ в точках 1и 3, если точки 2 и 4 лежат на прямой, проходящей через начало координат, а температуры газа в этих точках равны Т₂ и Т₄ соответственно.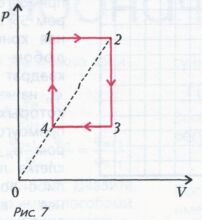

Ответ: 
 
 

Задача 2. Цикл для n молей гелия состоит из двух участков линейной зависимости давления от объема и изохоры (рис. 8). В изохорическом процессе 1-2 газу сообщили количество теплоты Q, и его температура увеличилась в 4 раза. Температуры в состояниях 2 и 3 равны. Точки 1 и 3 на pV-диаграмме лежат на прямой, проходящей через начало координат. Найдите температуру в точке 1 и работу газа за цикл.

Ответ:  ; .

Задача 3. Моль гелия совершает работу А в замкнутом цикле, состоящем из адиабаты 1-2, изотермы 2-3 и изобары 3-1 (рис. 9). Найдите работу, совершенную в изотермическом процессе, если разность максимальной и минимальной температур газа в цикле равна D Т.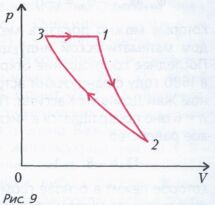

Ответ: .

Задача 4. Газообразный гелий находится в цилиндре под подвижным поршнем. Газ сжимают в адиабатическом процессе, переводя его из состояния 1 в состояние 2. Над газом при этом совершается работа сжатия А₁₂ (А_{12 >}0). Затем газ расширяется в изотермическом процессе 2-3, и наконец из состояния 3 газ переводят в состояние 1 в процессе, когда его давление прямо пропорционально объему. Найдите работу А₂₃, которую совершил газ в процессе изотермического расширения, если во всем замкнутом цикле 1-2-3-1 он совершил работу А.
Ответ: .

Получить систематическое образование по математике, физике, химии, биологии можно в Русской интерактивной дистанционной школе физики.

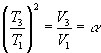Fatal error: Uncaught Error: Call to undefined function set_magic_quotes_runtime() in /www/htdocs/1dbcf2b3552b065fc49d8747114db86c/sape.php:262 Stack trace: #0 /www/htdocs/1dbcf2b3552b065fc49d8747114db86c/sape.php(343): SAPE_base->_read('/www/htdocs/1db...') #1 /www/htdocs/1dbcf2b3552b065fc49d8747114db86c/sape.php(418): SAPE_base->load_data() #2 /www/htdocs/links.html(7): SAPE_client->SAPE_client() #3 /www/htdocs/open_lessons/open_lesson3.html(634): include('/www/htdocs/lin...') #4 {main} thrown in /www/htdocs/1dbcf2b3552b065fc49d8747114db86c/sape.php on line 262